Obtención de las ecuaciones del movimiento de una aeronave
En este apartado se exponen los pasos a seguir y los principales resultados alcanzados. Para más detalle se dirige al lector al capítulo 5 de la memoria.
Arquitectura general
En el desarrollo de cada uno de los seis experimentos planteados se ha seguido una estructura similar:
- Obtención de las ecuaciones de la mecánica de vuelo y adimensionalización/normalización de las mismas en ejes viento. Tal y como se detallará más adelante, eliminar las dimensiones o normalizar los valores entre 0 y 1 permite que el algoritmo calcule de manera más precisa los términos que intervienen en la ecuación.
- Generación de las trayectorias sintéticas: en este paso se generan mediante software trayectorias sintéticas a partir de datos físicos de la aeronave o valores ya conocidos, como es la superficie alar o la densidad del aire. Para ello, se implementan las ecuaciones de la aeronave para unas condiciones iniciales aleatorias, con densidad de probabilidad uniforme en un rango que se especificará en cada caso. A continuación, se normalizan/adimensionalizan, según el caso, vía software (dividiendo entre la velocidad máxima) y se añade ruido. También se obtiene una trayectoria de validación que será utilizada para medir el error obtenido.
- Creación y entrenamiento del modelo de SINDy: una vez generadas las trayectorias, se elige la librería de funciones a utilizar, el optimizador y, si es necesario, las restricciones y suposición inicial. Por último se entrena el modelo de SINDy para obtener las ecuaciones que mejor se adaptan a los datos proporcionados.
- Evaluación de resultados: una vez obtenido el modelo que SINDy considera más adecuado se evalúan cualitativamente las ecuaciones obtenidas verificando que tienen los términos adecuados, se prueban las trayectorias obtenidas por dicho modelo obteniendo el error entre la trayectoria proporcionada por el algoritmo y la sintética y, en algunos casos, se calcula el error cuadrático entre los coeficientes del modelo que obtiene SINDy y los valores esperados.
- Variación de las entradas y parámetros que el algoritmo permite configurar, detallados en el este enlace. El objetivo es comprobar cómo afecta la variación de estas entradas en el desempeño del modelo calculado.
A continuación se muestra en pseudocódigo la implementación de los pasos anteriores.
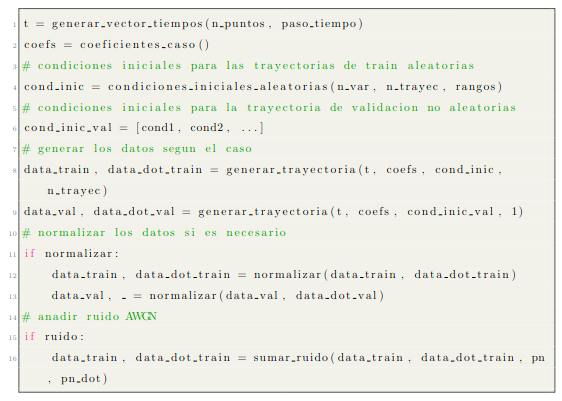
El código indicado más arriba se encarga de implementar el paso 2 de la lista anterior. En primer lugar, se genera el vector de tiempos y coeficientes para el desarrollo del caso. En segundo lugar, se generan condiciones iniciales aleatorias con densidad de probabilidad uniforme, según el número de incógnitas y trayectorias elegidas, para los datos de entrenamiento, y no aleatorias (deterministas) para los datos de validación, utilizados para medir el error en la trayectoria. En tercer lugar y utilizando estas condiciones iniciales, los coeficientes de la ecuación, el vector de tiempos generado y especificando el número de trayectorias, se genera la matriz de datos, así como la de derivadas,
. Los siguientes pasos consisten en normalizar la trayectoria (dividiendo entre la velocidad máxima de la misma) y sumarle ruido, según el caso.
Para la generación del ruido se ha considerado ruido aditivo, blanco y gaussiano (AWGN en inglés) que es utilizado para contaminar la matriz y
. Para generarlo se ha normalizado dicho ruido con respecto a la potencia de la señal, de manera que la potencia del ruido representa
veces la potencia de la señal original.
En el código mostrado a continuación se implementan los pasos 3 y 4 de la estructura anterior, los cuales se encargan de crear el modelo, entrenarlo y evaluar los resultados obtenidos. El primer lugar, se crea la librería de funciones a utilizar por el algoritmo para la obtención de las ecuaciones. Conocidas las funciones que componen la librería es posible obtener la matriz de coeficientes que debería obtener SINDy. En segundo lugar, se obtienen las restricciones y suposición inicial, si se requiere. En tercer lugar, se crea el modelo de SINDy mediante la sentencia
ps.SINDy, donde ps es un alias para la librería PySINDy, especificando el optimizador, suposición inicial, restricciones, librería de funciones y nombre de las variables. En cuarto lugar, se alimenta al modelo con los datos generados en el código anterior. A continuación, se calcula la trayectoria que simula el algoritmo para las ecuaciones que ha devuelto dada la condición inicial de la trayectoria de validación. Por último, se calcula el error cuadrático medio de los coeficientes de la ecuación y el error entre las trayectorias de validación real y simulada.

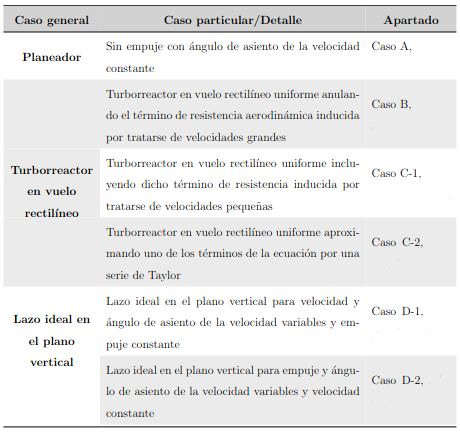
Casos desarrollados de aeronaves
En la tabla que se muestra a continuación se agrupan los diversos casos realizados sobre trayectorias de aeronaves
Caso A
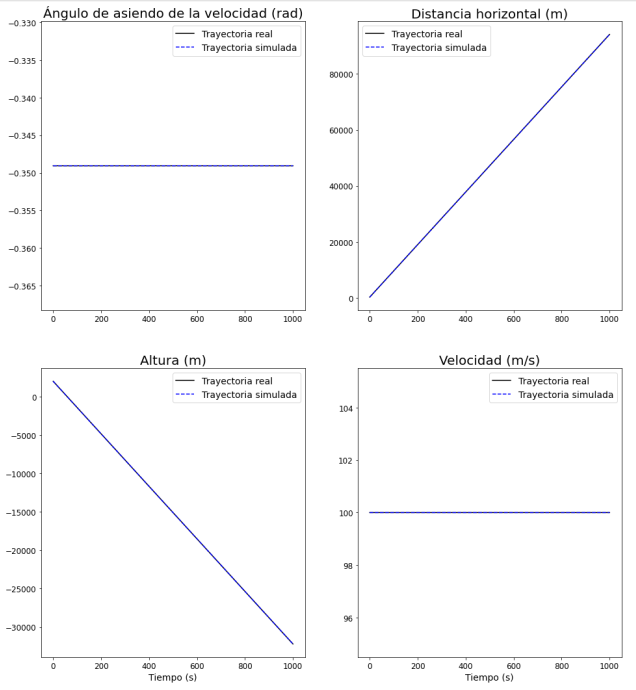
Este primer caso es el más sencillo que se ha desarrollado y el objetivo es familiarizarse con la implementación de las ecuaciones de la mecánica de vuelo vía software y entender el funcionamiento del algoritmo. En este caso no se adimensionalizan o normalizan las ecuaciones debido a su simplicidad.
Se pretende implementar el vuelo de un planeador (sin empuje) con un ángulo de asiento de la velocidad y velocidad aerodinámica uniformes. Este es el único caso en el que se obtienen las ecuaciones cinemáticas. Se ha decidido llevar a cabo este enfoque por ilustrar un ejemplo de implementación de estas ecuaciones y no de las dinámicas.
En la imagen que se muestra a continuación se puede ver la trayectoria sintética de la aeronave, la predicha por el algoritmo y las ecuaciones obtenidas por el mismo.
Caso B
En este caso se modela un vuelo con empuje orientado según el sentido que indica el eje y describiendo un vuelo rectilíneo, uniforme y simétrico, por lo que el ángulo de asiento de la velocidad,
, es nulo.
Se sustituye el valor de por su expresión
se despeja de la ecuación dinámica del eje
el coeficiente de sustentación,
. A continuación, se incluye la resistencia aerodinámica por la expresión
+
en la ecuación del eje
y se sustituye el
en el término de resistencia aerodinámica inducida. Agrupando los términos constantes, asumiendo velocidades grandes y normalizando la ecuación de la velocidad por la relación
se obtiene la siguiente ecuación que modela el comportamiento de la aeronave
,
donde y
Al alimentar al algoritmo SINDy con trayectorias sintéticas que siguen la cuación anterior se obtiene la siguiente trayectoria simulada junto al sistema de ecuaciones predicho:
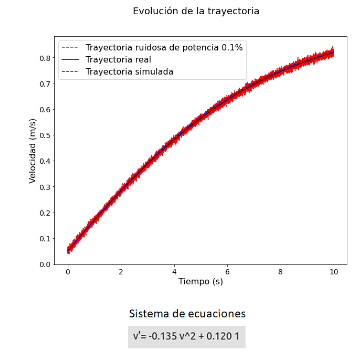
Caso C-1
En este caso y a diferencia del anterior, se cosideran velocidades pequeñas, por lo que el término de la resistencia dependiente de ya no se puede despreciar de la ecuación. La ecuación que modela este movimiento es la siguiente.
,
donde y
y
siguen las expresiones detalladas en el caso anterior C-1.
Al alimentar al algoritmo SINDy con trayectorias sintéticas que siguen la cuación anterior se obtiene la siguiente trayectoria simulada junto al sistema de ecuaciones predicho:
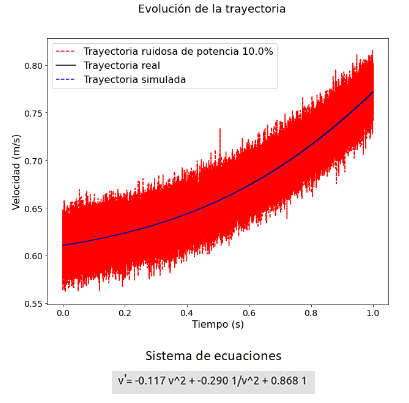
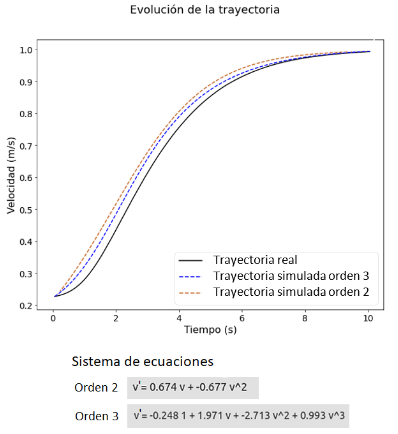
Caso C-2
En este caso se pretende obtener la ecuación desarrollada en el caso anterior para velocidades pequeñas pero aproximando el término por una aproximación en serie de Taylor de orden 2 y 3. Por tanto, la ecuación aproximada para orden 2 sería la siguiente
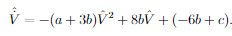
y para orden 3
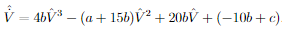
Al alimentar al algoritmo SINDy con trayectorias sintéticas que siguen la cuación anterior se obtiene la siguiente trayectoria simulada junto al sistema de ecuaciones predicho:
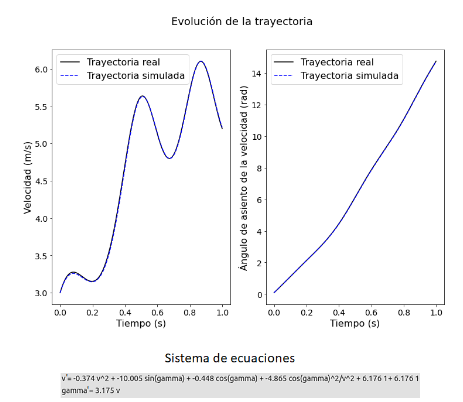
Caso D-1
En este casos las variables dependientes del tiempo son la velocidad y el ángulo de asiento de la velocidad, . Primeramente, se ha tratado de alimentar al algoritmo con trayectorias normalizadas. Sin embargo, los resultados obtenidos no han sido satisfactorios y es necesario realizar otras transformaciones a las ecuaciones. Para ello, se adimensionaliza la ecuación de la velocidad por un tiempo característico
y una velocidad característica
.
Se mantiene la definición y se incorporan las siguientes
.
Sustituyendo las expresiones anteriores en las ecuaciones dinámicas y y eligiendo cuidadosamente la velocidad característica se obtiene el siguiente sistema de ecuaciones
,
donde los coeficientes son constantes y vienen representados por las siguientes expresiones
+
.
Al alimentar al algoritmo SINDy con trayectorias sintéticas que siguen la cuación anterior se obtiene la siguiente trayectoria simulada junto al sistema de ecuaciones predicho:
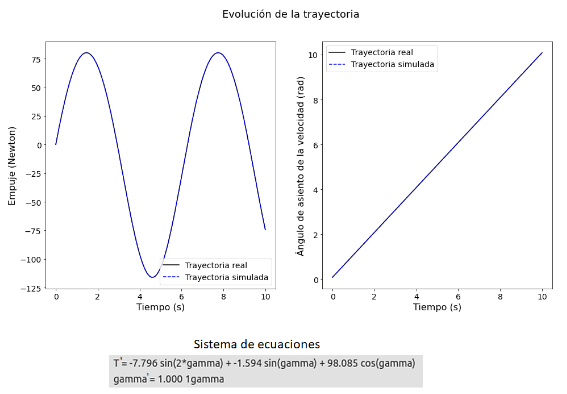
Caso D-2
En este caso las incógnitas dependientes del tiempo son ,
y
que quedan descritas por 3 ecuaciones, dos ecuaciones dinámicas y una ecuación angular
. Nótese que la velocidad es constante en este caso. Desarrollando dichas ecuaciones y agrupando términos se obtiene el siguiente sistema formado por dos ecuaciones
,
donde
.
Al alimentar al algoritmo SINDy con trayectorias sintéticas que siguen la cuación anterior se obtiene la siguiente trayectoria simulada junto al sistema de ecuaciones predicho:
Resultados
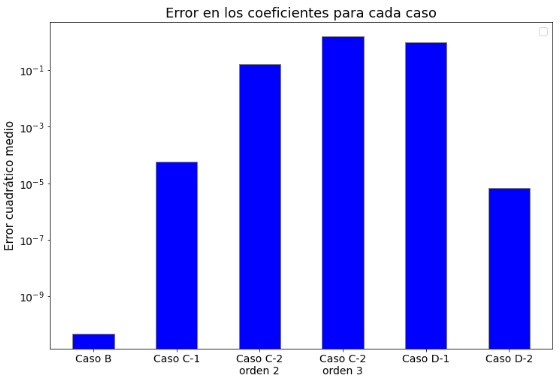
Para concluir este capítulo se representa en la siguiente tabla una comparativa entre las ecuaciones teóricas y las ecuaciones obtenidas por el algoritmo y el error cuadrático medio en los coeficientes. Esta tabla, al igual que el gráfico de barras localizado al final de este apartado se han generado utilizando 20 trayectorias para los datos de entrenamiento. De nuevo, para aumentar la robustez de los resultados se ha repetido todo el proceso de generación de datos, creación del modelo, entrenamiento del mismo y validación de resultados en diez ocasiones y se muestra la mediana del error de estas diez ejecuciones.
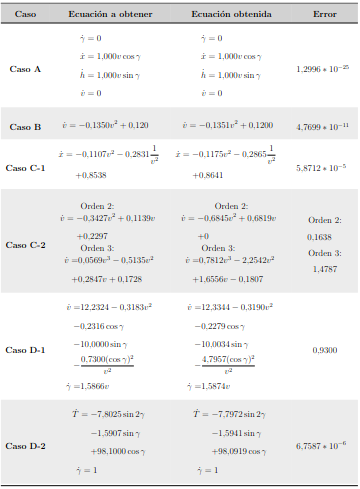
En dicha tabla se puede observar que de manera general el algoritmo es capaz de recuperar correctamente las ecuaciones, mostrando un error en los coeficientes de las mismas bajo. Sin embargo, en el caso C-2, tanto para la aproximación de orden 2 como de orden 3, se puede ver que el error asociado es mayor. Esto puede ser debido a que el algoritmo es alimentado con trayectorias que siguen la ecuación del caso C-1 en la tabla pero se utiliza una librería polinómica de grado 2 y 3 en la que no aparece el término . El algoritmo, en lugar de obtener los coeficientes asociados al desarrollo en serie de Taylor entorno al punto 1, trata de aproximar la trayectoria en todos los puntos, la cual no ha sido generada utilizando esta aproximación. Esto se confirma si vemos el error asociado a los coeficientes en la tabla y el error asociado a la trayectoria, ver gráfica de la trayectoria del caso C-2, estos difieren considerablemente.
Por otro lado, vemos que para el caso D-1 el error asociado a los coeficientes es mayor que el caso homólogo D-2, esto es debido a que el coeficiente asociado al término no es detectado correctamente por el algoritmo.
En el gráfico de barras se representa el error cuadrático medio de los coeficientes de las ecuaciones teóricas y predichas representadas en la tabla anterior. No se ha incluido el caso A debido a que la estimación de los coeficientes era perfecta, y el error que mostraba era debido a la resolución del ordenador, obstaculizando la correcta visualización de los órdenes de magnitud del resto de casos.